计算机图形学入门：点，向量，法线（译文）

Swedish li in Toykyo

2020年08月13日

原文：Points, Vectors and Normals (opens new window)

点、向量、矩阵和法线是计算机图形学（GC）的基础，就像字母和文学的关系一样；因此很多计算机图形学的书都把线性代数和几何做为开始篇章。但是对于很多希望学习图形编程的人来说在他们进行图形绘制之前面对大量的数学知识是令人沮丧的。如果你不愿意学习图形编程的原因是面对数学的不适或尚未理解矩阵，请不要在这里放弃。

在我们已经开设的“3D 渲染基础”部分有一系列不需要任何预备线性代数知识的课程。我们相信以实践和有趣的东西开始学习是令人兴奋的，因此我们选择了一个相当不正式的方式来教授 CG 编程技术；例如一个介绍性的光线追踪器，它只需要少量的数学知识和一些编程知识。编写一个渲染器是一个令人兴奋和有效的学习数学的方式，因为你可以渐进的观察到某些东西如何被变成具体的结果（例如你最终绘制的图片）。在我们绘制 CG 图片的时候，点、向量和矩阵的基石作用将被逐渐说明；我们讲在每个课程中大量广泛的使用他们。

在这个课程中，你将学到他们是如何构造的、如何工作，以及可以操作他们的各种技术。这个课程我们也会讲解各种在线性代数、CG 研究者中常年在解决问题和编写代码中使用的规约。你应该注意这些规约，因为他们经常会在书籍中被提及（并且在网络上只很少的资料）。这些规约非常重要；在你阅读或使用其他开发者的代码或技术的时候，你必须先知道他们正在使用什么样的规约。

在我们开始之前先做一个简单的提示。如果你是一个数学纯粹主义者，你将会对这里解释的技术与线性代数无关感到奇怪。我们将保持这个课程范围的广泛性，同时包括简单的、在 CG 领域常用的数学技术，这些将和向量和矩阵仅有松散的关联性。例如，从数学角度来说一个点和线性代数（一个关注向量的数学分支）没有什么相关性。我们选择覆盖点的原因是因为点在计算机图形学中太过常见了（并且来自线性代数中的同样方法也可以操作它们）。如果你尚未理解点和向量之间的差别，请不要担心，我们将在这章中广泛讨论这些。

# 什么是线性代数？关于向量

如何确切的描述线性代数？我们将在这个课程中学习到什么？正如我们在前一章节提到的，线性代数是一个研究向量的数学分支。现在你可能会问：”什么是向量，它为什么在计算机图形学中很有用？“我们将不会深入探讨许多细节，但你应该知道向量可以使用一个数字序列来表示。这个可以拥有任意长度的数字序列在数学中有时也被称作元组（tuple）。如果你像指定向量的这个长度，你可以说 n 元组(n-tuple),这里的 n 表示的是元素的数量向量。下边的示例是一个 6 元素向量的数学符合的表示。

$V = (a,b,c,d,e,f)$

这里的 a, b, c, d, e, f 为实数。

将这些数字组合在一起的想法是让它们在一个问题的上下文中表示一个有意义的量或概念。例如，在计算机图形领域向量可以表示空间中的一个位置或者方向。
我们可以用一系列强大且严谨的方式对这些向量进行变换。这个对向量的内容进行转换的执行过程被称作线性变换。我们将在下面的章节花费大量的时间讨论这个变换；现在，你只需要知道它们是非常有用的就可以了。

# 点和向量

点和向量的应用贯穿于很多科学领域的诸多背景之下。在这个部分，我们将对和这个教程和计算机图形学相关的部分进行讲解。

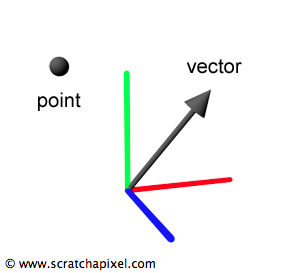
在这里，一个点表示一个三维空间中的位置。另一方面，一个向量常常代表一个在三维空间中的方向(相对的幅度或大小)。向量可以被看做指向很多方向的箭头。三维的点和坐标当然也可以用前面提到的元组相似的方式来表示。

$V = (x,y,z)$

这里的(x,y,z)为实数。

点是空间中位置的描述，向量可以看做是一个方向

当我们和一个数学家或物理学家对话的时候要注意，他们理解中的向量或点更加一般化；他们没有必要像我们一样在 CG 中那样对它们进行限制。对它们来说，一个向量可以是随意的，甚至可以用任何数量的数字来表示。

我们将在简单的介绍完同质点后结束这个章节。有时我们会为了数学上的便利去在点的表示上添加第四个元素。下面一个包含同质坐标的点表示:

$P_H = (x,y,z,w)$

在将点和矩阵相乘的时候会使用到同质点。你不需要担心你在这个课程这个阶段和不理解它。我们在这里提到它的原因是有时候在文献中会出现这些，这可能会让你感到迷惑。它将会在之后的课程中做详细介绍。

# 关于变换的简单介绍

你可能仍然想知道线性变换可以对点和向量产生什么样的影响。事实上这非常简单。在CG中点上最常见的操作之一就是简单的在空间中移动它们。这种变换被更具体的称作**平移（translation）**并且在渲染的过程中起到了非常重要的作用。

平移操作就是对原始点（可以看作一个输入的位置点）的的线性变换。对于一个向量（你应该记得，这是一个方向）来说，平移式没有意义的。这是因为向量的开始位置（即居中位置）并不重要。五年在什么位置的“箭头”，只要拥有相同的长度，指向相同的方向，它们就是相等的。相反的，我们经常向量上使用另一种线性变换：旋转。有很多常见的操作可以使用，但对于现在来说，让我们只考虑如何对一个点进行平移，对一个向量进行旋转。

$\begin{alignedat}{5} P & \rarr Translate & \rarr P_T \\ V & \rarr Rotate & \rarr V_T \end{alignedat}$

在这里下标字母 T 代表 变换

你可能已经注意到，到这里我们还没有讨论向量的长度，或着说是大小的含义。实际上，箭头（向量）的长度在 CG 中非常重要。当一个向量的长度正好为 1 时，我们就说这个向量已经归一化（你将会经常听到这个术语）

归一化的向量操作包括将向量的长度变为 1，但保持方向不变。在大多数的时间，我们希望向量是归一化的。但是在一些情况中，可能更倾向于使用非归一化的向量，因为向量的长度有时候是有意义的。

例如，想象一下你用一条线连接了点 $A$ 和点 $B$ 。从某种意义上说这条线所创建的向量显示了点 $B$ 到点 $A$ 的相对位置。这意味着它给出了你站在点 $A$ 所在的位置时点 $B$ 所在的方向。在这个例子中向量的长度表示点 $A$ 到点 $B$ 的距离。这个距离在某些时候在特定的算法中是需要的。

向量的归一化经常是应用程序中错误的源头，并且在你每一次声明（或使用）一个变量的时候，我推荐你有意识的文一下你自己这个向量是否是一个归一化的向量或者是否应该被归一化。

# 法线

a normal is perpendicular to the plane tangent a P.

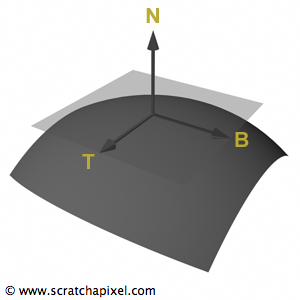
法线在计算机图形学（或几何学）中是一个技术术语，用来描述几何对象表在该表面上某个点的方向。从技术上来讲，在曲面 $P$ 点处的曲面法线可以被看作是在曲面的点 $P$ 处的切面相垂直的向量。法线在明暗处理中起着重要的作用，它们被用来计算对象的亮度（这一部分可以参考后边的光线和明暗处理课程）。

法线可以被看做是向量，但又一点要注意：它们的变换方式于向量不同。这是我们要在这里花时间区分它们的主要原因。你将会在“法线变换”这个章节找到更多关于这方面的信息。对于现在，最重要的是你要理解它们是什么。

# 从理论到 C++

在我们的 C++ 代码中，不会对点，向量，法线进行区分；我们使用一个类 Vec3 （一个模板类，可以根据你的需要来创建 float, int, double 的版本）来表示这三者。有些开发者倾向于区分它们。这显然降低了发生错误的可能性。根据经验，我们发现只用一个类来处理这些（就像 OpenEXR 库那样）会更加高效（在开始的时候我们可以写较少的代码）。然而，我们仍然需要小心的对待我们正在处理的Vec3对象，通过调用一些特定的函数来判断它是否代表一个点，一个向量，或一个法线。你应该还记得，这在我们使用变换的时候尤为重要。完整的代码将在课程的下载部分提供。

template<typename T>
class Vec3
{
public:
    // 3个初始化向量的基本方式
    Vec3() : x(T(0)), y(T(0)), z(T(0)) {}
    Vec3(const T &xx) : x(xx), y(xx), z(xx) {}
    Vec3(T xx, T yy, T zz) : x(xx), y(yy), z(zz) {}
    T x, y, z;
};

typedef Vec3<float> Vec3f;

Vec3<float> a;
Vec3f b;

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

# 摘要

从第一章开始，你应该记住在数学上向量可以是任意维度的。但在 CG 中，我们使用一个更加精确的定义：向量是3D空间中的方向（因此使用3个数字来表示）。另外，我们把空间中的位置用点来表示（在3D空间也同样使用3个数字来表示）。同质点（Homogeneous points）是一个特例，我们用4个数字来表示它，我们将会在稍后的章节来学习它。

点和向量都可以使用线性变换进行变换。

你会看到线性变换这个术语被经常使用。如果线在进行变换的同时保留了下来，我们就说这是线性变换（和一个矩阵相乘就是一次线性变换）。
典型的变换例子就是对点的平移（translation）和对向量的旋转（rotation）。向量的长度可以被设定为 1，我们称它为向量的归一化。向量的长度（在归一化之前）表示了两个点之间的距离，在某些特定的算法中需要它。由于这个原因，开发者必须谨慎的对待向量归一化的时机，和为什么要选择归一化向量。

# 接下来我们将学习什么？

定义点和向量的三个数字代表什么？这个重要的概念我们还没有进行解释。这些数字代表点相对一个参考点（有时候也被称作原点）的坐标（2D 或 3D 空间）。这个参考系被我们称作坐标系统，这将是我们在下一章的主题内容。

# 参考链接

Shading 浓淡处理 (opens new window)
浓淡处理（英语：Shading，也称明暗处理、着色法）是在三维模型或插画中通过不同的亮度表现深度的方法。